Determinant of a matrix cookiegaret

Determinants DETERMINANTS Our definition of determinants is as follows. If A = [a] is one by one, then det (A) = a. If A is the 2 by 2 matrix a b c d then det (A) = ad - bc. In the general case, we assume that one already knows how to compute determinants of size smaller than n by n. Let A be an n by n matrix. Then det (A) is defined as

Matrix Determinant Calculator 2x2 Deb Moran's Multiplying Matrices

Math 21b: Fact sheet about determinants. matrix A is a scalar, denoted det (A). [Non-square matrices do not have determinants.] The determinant of a square matrix A detects whether A is invertible: If det (A)=0 then A is not invertible (equivalently, the rows of A are linearly dependent; equivalently, the columns of A are linearly dependent.

Matrices and Determinants Formula Sheet and Summary Teachoo

The first is the determinant of a product of matrices. Theorem 3.2.5: Determinant of a Product. Let A and B be two n × n matrices. Then det (AB) = det (A) det (B) In order to find the determinant of a product of matrices, we can simply take the product of the determinants. Consider the following example.

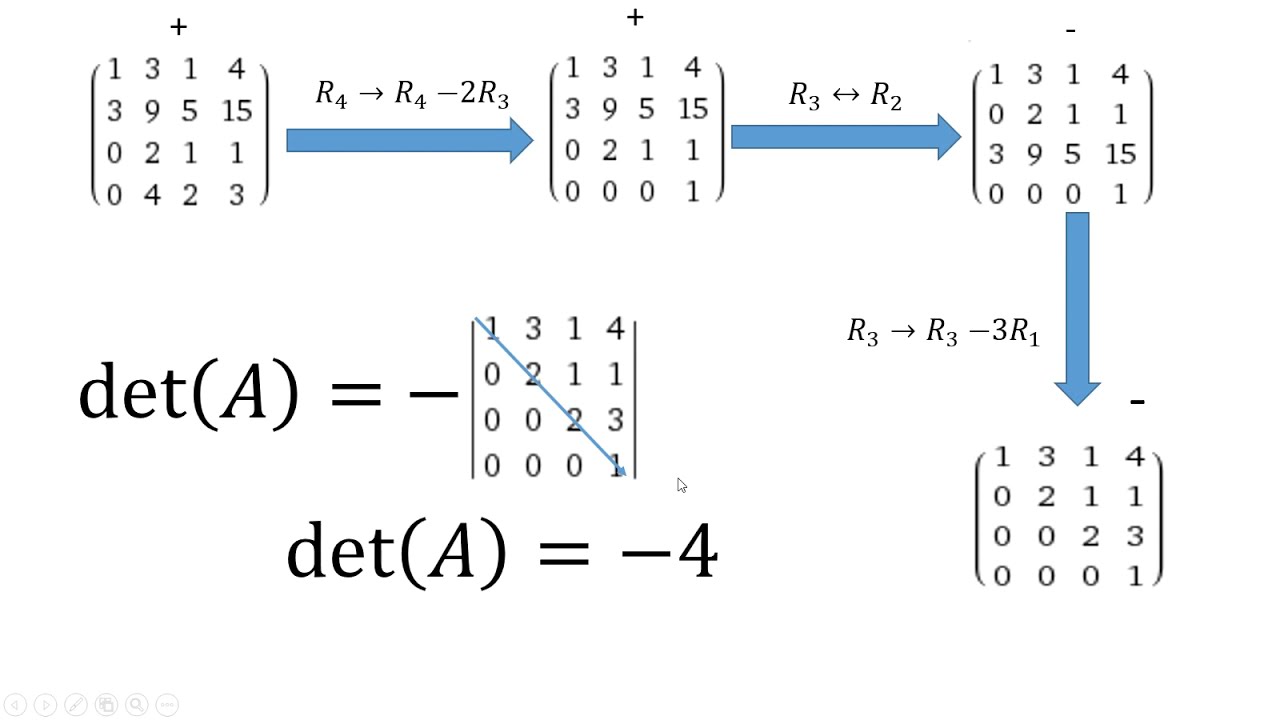
How to Find The Determinant of a 4x4 Matrix (Shortcut Method) YouTube

Since the identity matrix is diagonal with all diagonal entries equal to one, we have: \[\det I=1.\] We would like to use the determinant to decide whether a matrix is invertible. Previously, we computed the inverse of a matrix by applying row operations. Therefore we ask what happens to the determinant when row operations are applied to a matrix.

Solved For the n x n matrix compute det (A + tI) where I is

Definition 2.6.1 2.6. 1: The Inverse of a Matrix. A square n × n n × n matrix A A is said to have an inverse A−1 A − 1 if and only if. AA−1 = A−1A = In A A − 1 = A − 1 A = I n. In this case, the matrix A A is called invertible. Such a matrix A−1 A − 1 will have the same size as the matrix A A. It is very important to observe.

Determinant of a 3 by 3 matrix YouTube

In the resulting matrix, the \(i\)th row is zero, so \(\det(A) = 0\) by the first part. Still assuming that \(A\) is upper-triangular, now suppose that all of the diagonal entries of \(A\) are nonzero. Then \(A\) can be transformed to the identity matrix by scaling the diagonal entries and then doing row replacements:

What Is The Determinant Of An Identity Matrix Johnathan Dostie's Multiplying Matrices

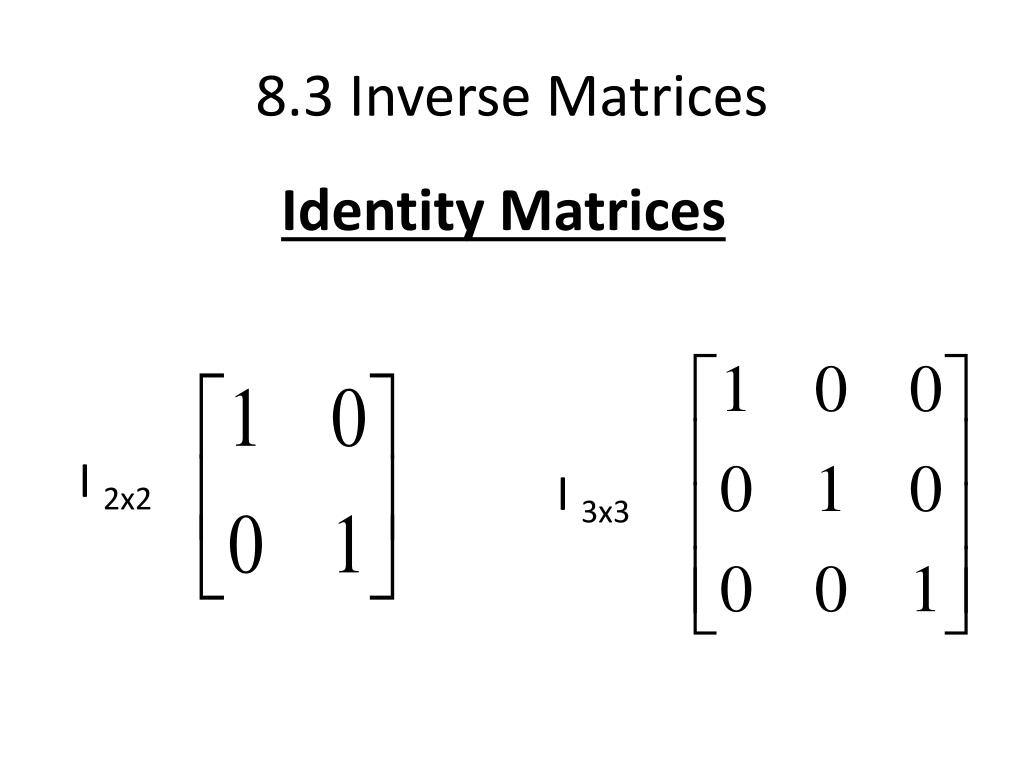
An Identity Matrix is a square matrix of any order whose principal diagonal elements are all ones and the rest other elements are all zeros. In this lesson, we will look at what identity matrices are, how to find different identity matrices, some properties of identity matrices, and the determinant of an identity matrix.

Identity Matrix

For matrices with other dimensions you can solve similar problems, but by using methods such as singular value decomposition (SVD). 2. No, you can find eigenvalues for any square matrix. The det != 0 does only apply for the A-λI matrix, if you want to find eigenvectors != the 0-vector.

PPT Chapter 8 Matrices and Determinants PowerPoint Presentation, free download ID2690088

The reduced row echelon form of the matrix is the identity matrix I 2, so its determinant is 1. The second-last step in the row reduction was a row replacement, so the second-final matrix also has determinant 1. The previous step in the row reduction was a row scaling by − 1 / 7; since (the determinant of the second matrix times − 1 / 7) is 1, the determinant of the second matrix must be.

How to Find the Determinant of a 5x5 Matrix YouTube

Determinant of the Identity Matrix proof Asked 7 years, 8 months ago Modified 7 years, 8 months ago Viewed 27k times 2 I have trouble proving that for all n n, det(In) = 1 det ( I n) = 1 In I n is Identity Matrix nxn n x n I tried to use Inductive reasoning but without any progress linear-algebra Share Cite Follow edited Apr 23, 2016 at 13:24

Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial YouTube

Identity Matrix Definition An identity matrix is a square matrix in which all the elements of principal diagonals are one, and all other elements are zeros. It is denoted by the notation "I n" or simply "I". If any matrix is multiplied with the identity matrix, the result will be given matrix. The elements of the given matrix remain unchanged.

linear algebra Origin and use of an identity of formal power series \det(1 \psi T) = \exp

Swapping two rows of a matrix does not change | det (A) |. The determinant of the identity matrix I n is equal to 1. The absolute value of the determinant is the only such function: indeed, by this recipe in Section 4.1, if you do some number of row operations on A to obtain a matrix B in row echelon form, then

PPT Matrices Inverse Matrix PowerPoint Presentation, free download ID5601422

Determinant of a Matrix. The determinant is a special number that can be calculated from a matrix. The matrix has to be square (same number of rows and columns) like this one: 3 8 4 6. A Matrix. (This one has 2 Rows and 2 Columns) Let us calculate the determinant of that matrix: 3×6 − 8×4. = 18 − 32.

PPT Matrix Algebra Basics PowerPoint Presentation, free download ID150371

1 The determinant of a permutation matrix P is 1 or −1 1 = −1. 0 depending on whether P exchanges an even or odd number of rows. From these three properties we can deduce many others: 4. If two rows of a matrix are equal, its determinant is zero. This is because of property 2, the exchange rule.

How to Evaluate the Determinant of a 3x3 Matrix Quick & Easy Method YouTube

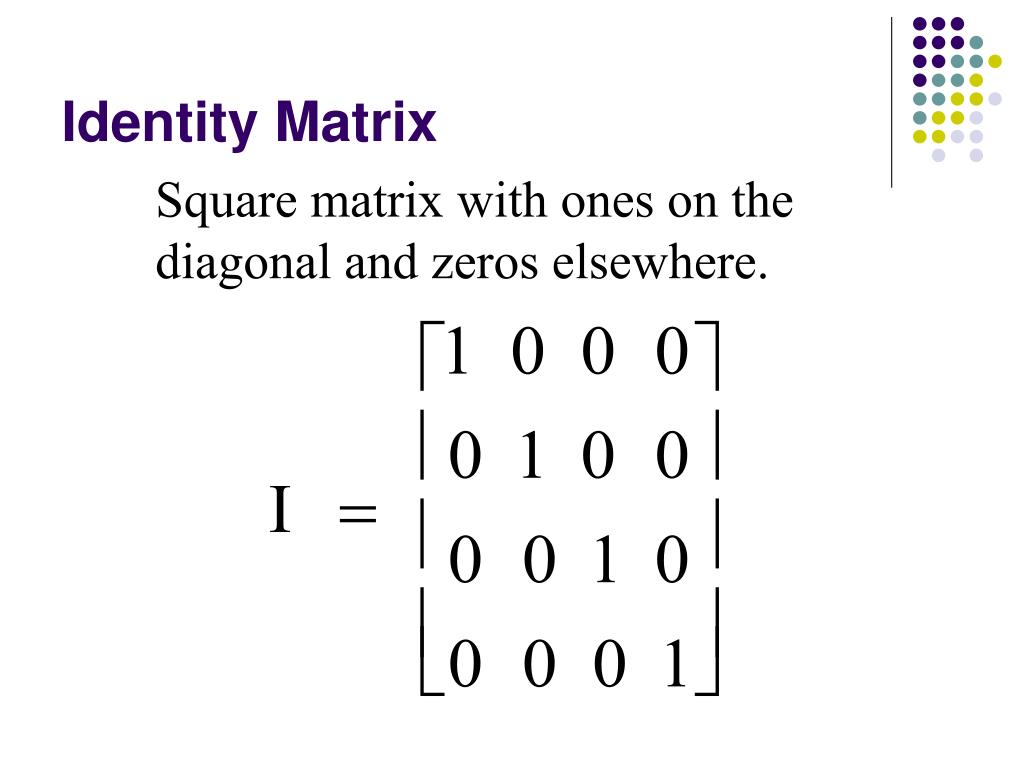
The n × n identity matrix, denoted I n , is a matrix with n rows and n columns. The entries on the diagonal from the upper left to the bottom right are all 1 's, and all other entries are 0 . For example: I 2 = [ 1 0 0 1] I 3 = [ 1 0 0 0 1 0 0 0 1] I 4 = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]

27.A square matrix of order n is both involuntary and idempotent matrix. The value of the

The identity matrix is the only idempotent matrix with non-zero determinant. That is, it is the only matrix such that: When multiplied by itself, the result is itself. All of its rows and columns are linearly independent. The principal square root of an identity matrix is itself, and this is its only positive-definite square root.